SOFA specifications: Difference between revisions

From Sofaconventions
Jump to navigation Jump to search
← Older editNewer edit →
Content deleted Content added
Testing math module
formulas edited
Line 106: Line 106:
The transfer function H(z) of a filter can be described as:
The transfer function H(z) of a filter can be described as:


H(z) = B1(z) / A1(z) . B2(z) / A2(z) . ... . Bp(z) / Ap(z)
<math>H(z) = \frac{B_1(z)}{A_1(z)} \cdot \frac{B_2(z)}{A_2(z)} \cdot ... \cdot \frac{B_p(z)}{A_p(z)}</math>


where p is the number of second order sections, A(z) is denominator representing the poles of a filter, and B(z) is numerator representing the zeros of a filter. Then, each SOS can be described as:
where <math>p</math> is the number of second order sections, <math>A(z)</math> is denominator representing the poles of a filter, and <math>B(z)</math> is numerator representing the zeros of a filter. Then, each SOS can be described as:


Bi(z) = bi,0 + bi,1 z^(-1) + bi,2 z^(-2)
<math>B_i(z) = b_{i,0} + b_{i,1} z^{-1} + b_{i,2} z^{-2}</math>


Ai(z) = ai,0 + ai,1 z^(-1) + ai,2 z^(-2)
<math>A_i(z) = a_{i,0} + a_{i,1} z^{-1} + a_{i,2} z^{-2}</math>


Note that usually, Ai(z) is normalized such that ai,0 = 1.
Note that usually, <math>A_i(z)</math> is normalized such that <math>a_{i,0} = 1</math>.


Thus, in the DataType SOS, a filter is represented by three mandatory variables:
Thus, in the DataType SOS, a filter is represented by three mandatory variables:
Line 121: Line 121:
* Data.Delay: broadband delay (in samples resulting from SamplingRate). Note: Use Delay of zero when not used.used).
* Data.Delay: broadband delay (in samples resulting from SamplingRate). Note: Use Delay of zero when not used.used).
* Data.SOS: list of coefficients of all SOSs.
* Data.SOS: list of coefficients of all SOSs.
** Size: Data.SOS has the size of '''[ M R N ]''' with N as the total number of coefficients, thus an integer multiple of 6 corresponding to 6p.
** Size: Data.SOS has the size of '''[ M R N ]''' with N as the total number of coefficients, thus an integer multiple of 6 corresponding to <math>6p</math>.
** Format of the list: Along the dimension N, the list goes like: [ b1,0 b1,1 b1,2 a1,0 a1,1 a1,2 b2,0 b2,1 b2,2 a2,0 a2,1 a2,2 .... bp,0 bp,1 bp,2 ap,0 ap,1 ap,2 ] which corresponds to [ B1(z) A1(z) B2(z) A2(z) .... Bp(z) Ap(z) ]
** Format of the list: Along the dimension N, the list goes like: <math>[ b_{1,0}\ b_{1,1}\ b_{1,2}\ a_{1,0}\ a_{1,1}\ a_{1,2}\ b_{2,0}\ b_{2,1}\ b_{2,2}\ a_{2,0}\ a_{2,1}\ a_{2,2}\ ... b_{p,0}\ b_{p,1}\ b_{p,2}\ a_{p,0}\ a{p,1}\ a_{p,2} ]</math> which corresponds to <math>[ B_1(z)\ A_1(z)\ B_2(z)\ A_2(z)\ ... B_p(z)\ A_p(z) ]</math>




Line 141: Line 141:
|Data.Delay||<nowiki>0</nowiki>||m||MR||double||Broadband delay (in samples resulting from SamplingRate)
|Data.Delay||<nowiki>0</nowiki>||m||MR||double||Broadband delay (in samples resulting from SamplingRate)
|}
|}

Test:

<math>\int\limits_a^x f(\frac{\alpha}{2}\,)\,dx</math>

Revision as of 18:25, 15 November 2015

Specifications

  • SOFA 1.0 is reflected by the AES69-2015 standard. It mostly corresponds to SOFA 0.6, which specs can be downloaded here. A document with SOFA 1.0 specs is under preparation.

Older specs:


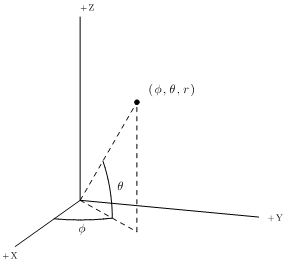
Coordinate system


Data Types

FIR (SOFA 1.0)

For storing impulse responses.

Note: Delay is mandatory (set to 0 if not used).

Name Default Flags Dimensions Type Comment
GLOBAL:DataType FIR rm attribute
Data.IR 0 m mRn double Impulse responses
Data.SamplingRate 48000 m I double Sampling rate of the samples in Data.IR
Data.SamplingRate:Units hertz m attribute Unit of the sampling rate
Data.Delay 0 m IR, MR double Additional delay of each IR (always in samples, i.e. units of N)


TF (SOFA 1.0)

Useful to describe a transfer function by a sparse number of frequencies. The guys from BEM simulations like it.

Note: the dimensional variable N is mandatory, it must be of dimension N, and must provide the frequency values.

Name Default Flags Dimensions Type Comment
GLOBAL:DataType TF rm attribute
Data.Real 0 m mRn double The real part of the complex spectrum
Data.Imag 0 m MRN double The imaginary part of the complex spectrum
N 0 m N double Frequency values
N_LongName frequency attribute
N_Units hertz m attribute Unit of the values given in N


FIRE (proposed)

FIRE is based on FIR and is intended for storing impulse responses which depend on the emitter (E).

Note: Delay is mandatory (set to 0 if not used).

Name Default Flags Dimensions Type Comment
GLOBAL:DataType FIRE rm attribute
Data.IR 0 m mREn double Impulse responses
Data.SamplingRate 48000 m I double Sampling rate of the samples in Data.IR
Data.SamplingRate:Units hertz m attribute Unit of the sampling rate
Data.Delay 0 m IRE, MRE double Additional delay of each IR (always in samples, i.e. units of N)


SOS (proposed)

This DataType stores a filter as a broadband delay and an arbitrary number of second order sections (SOSs).

The transfer function H(z) of a filter can be described as:

[math]\displaystyle{ H(z) = \frac{B_1(z)}{A_1(z)} \cdot \frac{B_2(z)}{A_2(z)} \cdot ... \cdot \frac{B_p(z)}{A_p(z)} }[/math]

where [math]\displaystyle{ p }[/math] is the number of second order sections, [math]\displaystyle{ A(z) }[/math] is denominator representing the poles of a filter, and [math]\displaystyle{ B(z) }[/math] is numerator representing the zeros of a filter. Then, each SOS can be described as:

[math]\displaystyle{ B_i(z) = b_{i,0} + b_{i,1} z^{-1} + b_{i,2} z^{-2} }[/math]

[math]\displaystyle{ A_i(z) = a_{i,0} + a_{i,1} z^{-1} + a_{i,2} z^{-2} }[/math]

Note that usually, [math]\displaystyle{ A_i(z) }[/math] is normalized such that [math]\displaystyle{ a_{i,0} = 1 }[/math].

Thus, in the DataType SOS, a filter is represented by three mandatory variables:

  • Data.SamplingRate: sampling rate used to describe the filter.
  • Data.Delay: broadband delay (in samples resulting from SamplingRate). Note: Use Delay of zero when not used.used).
  • Data.SOS: list of coefficients of all SOSs.
    • Size: Data.SOS has the size of [ M R N ] with N as the total number of coefficients, thus an integer multiple of 6 corresponding to [math]\displaystyle{ 6p }[/math].
    • Format of the list: Along the dimension N, the list goes like: [math]\displaystyle{ [ b_{1,0}\ b_{1,1}\ b_{1,2}\ a_{1,0}\ a_{1,1}\ a_{1,2}\ b_{2,0}\ b_{2,1}\ b_{2,2}\ a_{2,0}\ a_{2,1}\ a_{2,2}\ ... b_{p,0}\ b_{p,1}\ b_{p,2}\ a_{p,0}\ a{p,1}\ a_{p,2} ] }[/math] which corresponds to [math]\displaystyle{ [ B_1(z)\ A_1(z)\ B_2(z)\ A_2(z)\ ... B_p(z)\ A_p(z) ] }[/math]


Name Default Flags Dimensions Type Comment
Data.SOS permute([0 0 0 1 0 0],[3 1 2]) m mRn double Filter coefficients as SOS coefficients.
Data.SamplingRate 48000 m I double Sampling rate of the coefficients in Data.SOS and the delay in Data.Delay
Data.SamplingRate:Units hertz m attribute Unit of the sampling rate
Data.Delay 0 m MR double Broadband delay (in samples resulting from SamplingRate)
Retrieved from "https://www.sofaconventions.org/mediawiki/index.php?title=SOFA_specifications&oldid=1991"