SOFA specifications
Specifications
- SOFA 1.0 is reflected by the AES69-2015 standard. It mostly corresponds to SOFA 0.6, which specs can be downloaded here. SOFA 2.x specifications are defined in the the reaffirmed standards AES69-2020 and AES69-2022.
Older specs:
- Version 0.5: Download specifications
- Version 0.4: Discussion on the specifications (closed)
- Version 0.3: Download specifications
- Version 0.2: Specifications
- Version 0.1: Specifications as presented at the AES Convention 2013 in Rom
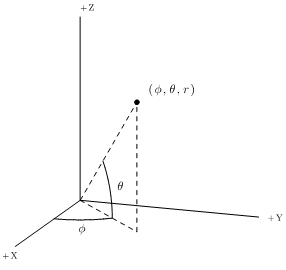
Coordinate system
SOFA 1.0 supports two coordinates systems: Cartesian and spherical in the azimuth/elevation representation.
SOFA 2.0 adds a spatially continuous representation of receivers by means of the coordinate type 'spherical harmonics'. To this end, data depending on the position of the receivers are stored as real-valued spherical harmonic coefficients along the dimension R. Thus, each subset of data for a specific R corresponds not to a specific receiver position, but to a specific spherical harmonic order and degree. Along the dimension R , the data are stored in the ACN order. The spatially continuous representation is indicated by the ReceiverPosition_Type of 'Spherical Harmonics', ReceiverPosition_Units is 'metre', and the ReceiverPosition stores the information about the radius only.
SOFA 2.0 further adds the spatially continuous representation of emitters, which uses the same scheme as that of receivers.
Data Types
SOFA 1.x
FIR
For storing impulse responses.
Note: Delay is mandatory (set to 0 if not used).
| Name | Default | Flags | Dimensions | Type | Comment |
|---|---|---|---|---|---|
| GLOBAL:DataType | FIR | rm | attribute | ||
| Data.IR | 0 | m | mRn | double | Impulse responses |
| Data.SamplingRate | 48000 | m | I | double | Sampling rate of the samples in Data.IR |
| Data.SamplingRate:Units | hertz | m | attribute | Unit of the sampling rate | |
| Data.Delay | 0 | m | IR, MR | double | Additional delay of each IR (always in samples, i.e. units of N) |
TF
Useful to describe a transfer function by a sparse number of frequencies. The guys from BEM simulations like it.
Note: the dimensional variable N is mandatory, it must be of dimension N, and must provide the frequency values.
| Name | Default | Flags | Dimensions | Type | Comment |
|---|---|---|---|---|---|
| GLOBAL:DataType | TF | rm | attribute | ||
| Data.Real | 0 | m | mRn | double | The real part of the complex spectrum |
| Data.Imag | 0 | m | MRN | double | The imaginary part of the complex spectrum |
| N | 0 | m | N | double | Frequency values |
| N_LongName | frequency | attribute | |||
| N_Units | hertz | m | attribute | Unit of the values given in N |
FIRE (deprecated)
FIRE is the proposed version of FIR-E. With FIR-E being standardized, we strongly discourage from using it, use FIR-E instead.
Note: Delay is mandatory (set to 0 if not used).
| Name | Default | Flags | Dimensions | Type | Comment |
|---|---|---|---|---|---|
| GLOBAL:DataType | FIRE | rm | attribute | ||
| Data.IR | 0 | m | mREn | double | Impulse responses |
| Data.SamplingRate | 48000 | m | I | double | Sampling rate of the samples in Data.IR |
| Data.SamplingRate:Units | hertz | m | attribute | Unit of the sampling rate | |
| Data.Delay | 0 | m | IRE, MRE | double | Additional delay of each IR (always in samples, i.e. units of N) |
SOFA 2.x
Datatypes standardized in SOFA 2.0 and SOFA 2.1:
FIR
For storing impulse responses.
Note: Delay is mandatory (set to 0 if not used).
| Name | Default | Flags | Dimensions | Type | Comment |
|---|---|---|---|---|---|
| GLOBAL:DataType | FIR | rm | attribute | ||
| Data.IR | 0 | m | mRn | double | Impulse responses |
| Data.SamplingRate | 48000 | m | I | double | Sampling rate of the samples in Data.IR |
| Data.SamplingRate:Units | hertz | m | attribute | Unit of the sampling rate | |
| Data.Delay | 0 | m | IR, MR | double | Additional delay of each IR (always in samples, i.e. units of N) |
FIR-E
FIR-E is based on FIR and is intended for storing impulse responses which depend on the emitter (E).
Note: Delay is mandatory (set to 0 if not used).
| Name | Default | Flags | Dimensions | Type | Comment |
|---|---|---|---|---|---|
| GLOBAL:DataType | FIR-E | rm | attribute | ||
| Data.IR | 0 | m | mREn | double | Impulse responses |
| Data.SamplingRate | 48000 | m | I | double | Sampling rate of the samples in Data.IR |
| Data.SamplingRate:Units | hertz | m | attribute | Unit of the sampling rate | |
| Data.Delay | 0 | m | IRE, MRE | double | Additional delay of each IR (always in samples, i.e. units of N) |
TF
Useful to describe a transfer function by a sparse number of frequencies. The guys from BEM simulations like it.
Note: the dimensional variable N is mandatory, it must be of dimension N, and must provide the frequency values.
| Name | Default | Flags | Dimensions | Type | Comment |
|---|---|---|---|---|---|
| GLOBAL:DataType | TF | rm | attribute | ||
| Data.Real | 0 | m | mRn | double | The real part of the complex spectrum |
| Data.Imag | 0 | m | MRN | double | The imaginary part of the complex spectrum |
| N | 0 | m | N | double | Frequency values |
| N_LongName | frequency | attribute | |||
| N_Units | hertz | m | attribute | Unit of the values given in N |
TF-E
TF-E is based on TF and is intended for storing impulse responses which depend on the emitter (E).
| Name | Default | Flags | Dimensions | Type | Comment |
|---|---|---|---|---|---|
| GLOBAL:DataType | TF-E | rm | attribute | ||
| Data.Real | 0 | m | mRnE | double | The real part of the complex spectrum |
| Data.Imag | 0 | m | MRNE | double | The imaginary part of the complex spectrum |
| N | 0 | m | N | double | Frequency values |
| N_LongName | frequency | attribute | |||
| N_Units | hertz | m | attribute | Unit of the values given in N |
SOS
This DataType stores a filter as a broadband delay and an arbitrary number of second order sections (SOSs).
The transfer function H(z) of a filter can be described as:
[math]\displaystyle{ H(z) = \frac{B_1(z)}{A_1(z)} \cdot \frac{B_2(z)}{A_2(z)} \cdot ... \cdot \frac{B_p(z)}{A_p(z)} }[/math]
where [math]\displaystyle{ p }[/math] is the number of second order sections, [math]\displaystyle{ A(z) }[/math] is denominator representing the poles of a filter, and [math]\displaystyle{ B(z) }[/math] is numerator representing the zeros of a filter. Then, each SOS can be described as:
[math]\displaystyle{ B_i(z) = b_{i,0} + b_{i,1} z^{-1} + b_{i,2} z^{-2} }[/math]
[math]\displaystyle{ A_i(z) = a_{i,0} + a_{i,1} z^{-1} + a_{i,2} z^{-2} }[/math]
Note that usually, [math]\displaystyle{ A_i(z) }[/math] is normalized such that [math]\displaystyle{ a_{i,0} = 1 }[/math].
Thus, in the DataType SOS, a filter is represented by three mandatory variables:
- Data.SamplingRate: sampling rate used to describe the filter.
- Data.Delay: broadband delay (in samples resulting from SamplingRate). Note: Use Delay of zero when not used.used).
- Data.SOS: list of coefficients of all SOSs.
- Size: Data.SOS has the size of [ M R N ] with N as the total number of coefficients, thus an integer multiple of 6 corresponding to [math]\displaystyle{ 6p }[/math].
- Format of the list: Along the dimension N, the list goes like: [math]\displaystyle{ [ b_{1,0}\ b_{1,1}\ b_{1,2}\ a_{1,0}\ a_{1,1}\ a_{1,2}\ b_{2,0}\ b_{2,1}\ b_{2,2}\ a_{2,0}\ a_{2,1}\ a_{2,2}\ ... b_{p,0}\ b_{p,1}\ b_{p,2}\ a_{p,0}\ a{p,1}\ a_{p,2} ] }[/math] which corresponds to [math]\displaystyle{ [ B_1(z)\ A_1(z)\ B_2(z)\ A_2(z)\ ... B_p(z)\ A_p(z) ] }[/math]
| Name | Default | Flags | Dimensions | Type | Comment |
|---|---|---|---|---|---|
| Data.SOS | permute([0 0 0 1 0 0],[3 1 2]) | m | mRn | double | Filter coefficients as SOS coefficients. |
| Data.SamplingRate | 48000 | m | I | double | Sampling rate of the coefficients in Data.SOS and the delay in Data.Delay |
| Data.SamplingRate:Units | hertz | m | attribute | Unit of the sampling rate | |
| Data.Delay | 0 | m | MR | double | Broadband delay (in samples resulting from SamplingRate) |