SOFA specifications: Difference between revisions

From Sofaconventions
Jump to navigation Jump to search
← Older editNewer edit →
Content deleted Content added
No edit summary
Line 41: Line 41:
|Data.Delay||<nowiki>0</nowiki>||m||IR, MR||double||Additional delay of each IR (always in samples, i.e. units of N)
|Data.Delay||<nowiki>0</nowiki>||m||IR, MR||double||Additional delay of each IR (always in samples, i.e. units of N)
|}
|}




=== TF (SOFA 1.0) ===
=== TF (SOFA 1.0) ===
Line 68: Line 70:
|N_Units||<nowiki>hertz</nowiki>||m||||attribute|| Unit of the values given in N
|N_Units||<nowiki>hertz</nowiki>||m||||attribute|| Unit of the values given in N
|}
|}




=== FIRE (proposed) ===
=== FIRE (proposed) ===
Line 93: Line 97:
|Data.Delay||<nowiki>0</nowiki>||m||IRE, MRE||double||Additional delay of each IR (always in samples, i.e. units of N)
|Data.Delay||<nowiki>0</nowiki>||m||IRE, MRE||double||Additional delay of each IR (always in samples, i.e. units of N)
|}
|}




=== SOS (proposed) ===
=== SOS (proposed) ===
Line 104: Line 110:
where p is the number of second order sections, A(z) is denominator representing the poles of a filter, and B(z) is nominator representing the zeros of a filter. Then, each SOS can be described as:
where p is the number of second order sections, A(z) is denominator representing the poles of a filter, and B(z) is nominator representing the zeros of a filter. Then, each SOS can be described as:


Bi(z) = bi0 + bi1 z^(-1) + bi2 z^(-2)
Bi(z) = bi,0 + bi,1 z^(-1) + bi,2 z^(-2)


Ai(z) = ai0 + ai1 z^(-1) + ai2 z^(-2)
Ai(z) = ai,0 + ai,1 z^(-1) + ai,2 z^(-2)


Note that usually, Ai(z) is normalized such that ai0 = 1.
Note that usually, Ai(z) is normalized such that ai,0 = 1.


Thus, in the DataType SOS, a filter is represented by three mandatory variables:
Thus, in the DataType SOS, a filter is represented by three mandatory variables:
Line 117: Line 123:


[ B1(z) A1(z) B2(z) A2(z) .... Bp(z) Ap(z) ] == [ b1,0 b1,1 b1,2 a1,0 a1,1 a1,2 b2,0 b2,1 b2,2 a2,0 a2,1 a2,2 .... bp,0 bp,1 bp,2 ap,0 ap,1 ap,2 ]
[ B1(z) A1(z) B2(z) A2(z) .... Bp(z) Ap(z) ] == [ b1,0 b1,1 b1,2 a1,0 a1,1 a1,2 b2,0 b2,1 b2,2 a2,0 a2,1 a2,2 .... bp,0 bp,1 bp,2 ap,0 ap,1 ap,2 ]





{| border="1"
{| border="1"

Revision as of 10:37, 12 May 2015

Specifications

  • SOFA 1.0 is reflected by the AES69-2015 standard. It mostly corresponds to SOFA 0.6, which specs can be downloaded here. A document with SOFA 1.0 specs is under preparation.

Older specs:


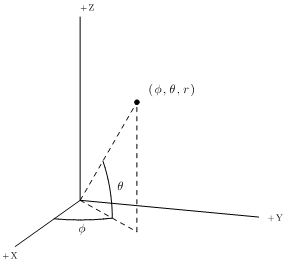
Coordinate system


Data Types

FIR (SOFA 1.0)

For storing impulse responses.

Note: Delay is mandatory (set to 0 if not used).

Name Default Flags Dimensions Type Comment
GLOBAL:DataType FIR rm attribute
Data.IR 0 m mRn double Impulse responses
Data.SamplingRate 48000 m I double Sampling rate of the samples in Data.IR
Data.SamplingRate:Units hertz m attribute Unit of the sampling rate
Data.Delay 0 m IR, MR double Additional delay of each IR (always in samples, i.e. units of N)


TF (SOFA 1.0)

Useful to describe a transfer function by a sparse number of frequencies. The guys from BEM simulations like it.

Note: the dimensional variable N is mandatory, it must be of dimension N, and must provide the frequency values.

Name Default Flags Dimensions Type Comment
GLOBAL:DataType TF rm attribute
Data.Real 0 m mRn double The real part of the complex spectrum
Data.Imag 0 m MRN double The imaginary part of the complex spectrum
N 0 m N double Frequency values
N_LongName frequency attribute
N_Units hertz m attribute Unit of the values given in N


FIRE (proposed)

FIRE is based on FIR and is intended for storing impulse responses which depend on the emitter (E).

Note: Delay is mandatory (set to 0 if not used).

Name Default Flags Dimensions Type Comment
GLOBAL:DataType FIRE rm attribute
Data.IR 0 m mREn double Impulse responses
Data.SamplingRate 48000 m I double Sampling rate of the samples in Data.IR
Data.SamplingRate:Units hertz m attribute Unit of the sampling rate
Data.Delay 0 m IRE, MRE double Additional delay of each IR (always in samples, i.e. units of N)


SOS (proposed)

This DataType stores a filter as a broadband delay and an arbitrary number of second order sections (SOSs).

The transfer function H(z) of a filter can be described as:

H(z) = B1(z) / A1(z) . B2(z) / A2(z) . ... . Bp(z) / Ap(z)

where p is the number of second order sections, A(z) is denominator representing the poles of a filter, and B(z) is nominator representing the zeros of a filter. Then, each SOS can be described as:

Bi(z) = bi,0 + bi,1 z^(-1) + bi,2 z^(-2)

Ai(z) = ai,0 + ai,1 z^(-1) + ai,2 z^(-2)

Note that usually, Ai(z) is normalized such that ai,0 = 1.

Thus, in the DataType SOS, a filter is represented by three mandatory variables:

  • SamplingRate: sampling rate used to describe the filter.
  • Delay: broadband delay (in samples resulting from SamplingRate). Note: Use Delay of zero when not used.used).
  • SOS: list of coefficients of all SOSs represented as a list:

[ B1(z) A1(z) B2(z) A2(z) .... Bp(z) Ap(z) ] == [ b1,0 b1,1 b1,2 a1,0 a1,1 a1,2 b2,0 b2,1 b2,2 a2,0 a2,1 a2,2 .... bp,0 bp,1 bp,2 ap,0 ap,1 ap,2 ]

Name Default Flags Dimensions Type Comment
Data.SOS [1 1] m mRn double Coefficients of the SOSs
Data.SamplingRate 48000 m I double Sampling rate of the samples in Data.SOS
Data.SamplingRate:Units hertz m attribute Unit of the sampling rate
Data.Delay [0 0] m MR double Monaural delay in samples
Retrieved from "https://www.sofaconventions.org/mediawiki/index.php?title=SOFA_specifications&oldid=1939"